深度學習中的優化技巧 - 批次 (Batch) 與動量 (Momentum)
批次 (Batch) 的運作機制
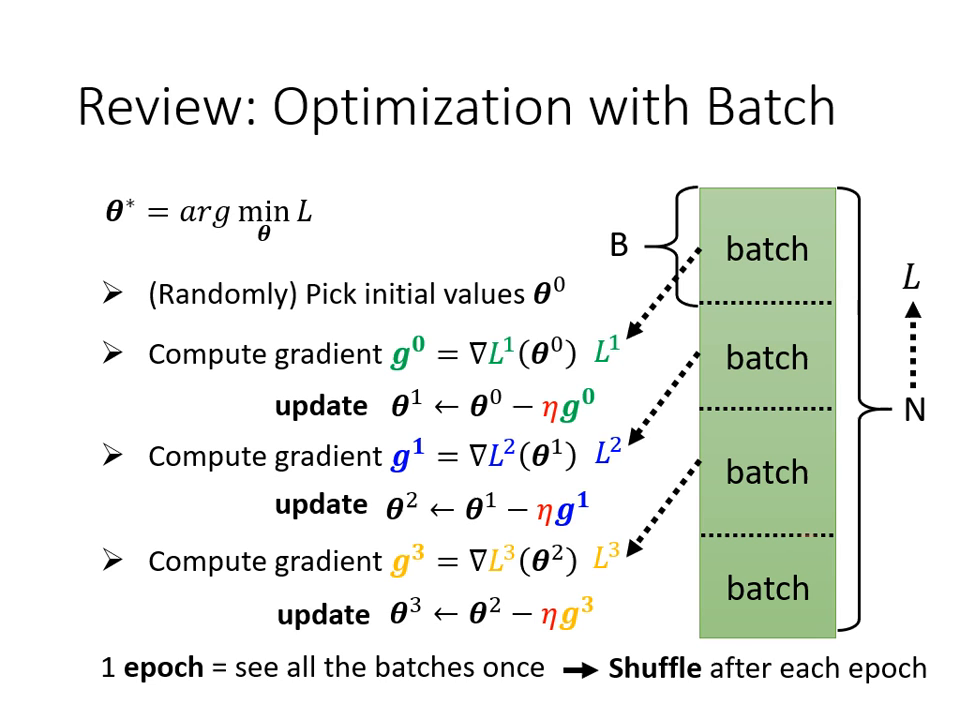
在訓練模型時,我們不會一次對所有資料(Full Batch)計算 Loss,而是將資料分成一個個小群組,稱為 Batch 或 Mini-batch。
- 訓練流程: 每次取出一個 Batch 的資料計算 Loss 和 Gradient,隨即更新一次參數。當所有 Batch 都被看過一遍,稱為完成一個 Epoch。
- 打亂資料 (Shuffle): 在每個 Epoch 開始前,通常會重新分配 Batch,確保每輪訓練時同一個 Batch 內的資料組合都不一樣。
大批次 (Full Batch) vs. 小批次 (Small Batch)
這兩者在「更新穩定度」與「訓練速度」之間存在權衡:
| 比較項目 | 大批次 (Full Batch / Large Batch) | 小批次 (Small Batch, 如 Batch Size = 1) |
|---|---|---|
| 更新速度 | 蓄力時間長,需看完所有資料才更新一次。 | 蓄力時間短,看一筆資料就更新一次。 |
| 穩定度 | 移動方向非常穩健。 | 移動方向曲折、帶有雜訊 (Noisy)。 |
| 平行運算 | GPU 擅長平行處理,Batch 大小在一定範圍內,運算時間幾乎相同。 | 無法發揮 GPU 平行處理優勢,跑完一個 Epoch 總時間較長。 |
| 效能表現 | 容易卡在臨界點 (Optimization 問題)。 | 較佳。 雜訊有助於跳出局部最小值或鞍點。 |

- 關鍵發現: 雖然大批次在 GPU 加持下「跑完一個 Epoch」的速度較快,但小批次在訓練集與測試集上的準確率通常更好。
為什麼「有雜訊」的小批次反而更好?
- 優化 (Optimization) 面: 不同的 Batch 有各自的 Loss Function。如果某個 Batch 讓梯度變為零(卡住),另一個 Batch 的梯度可能還有值,這能幫助模型「逃離」臨界點。
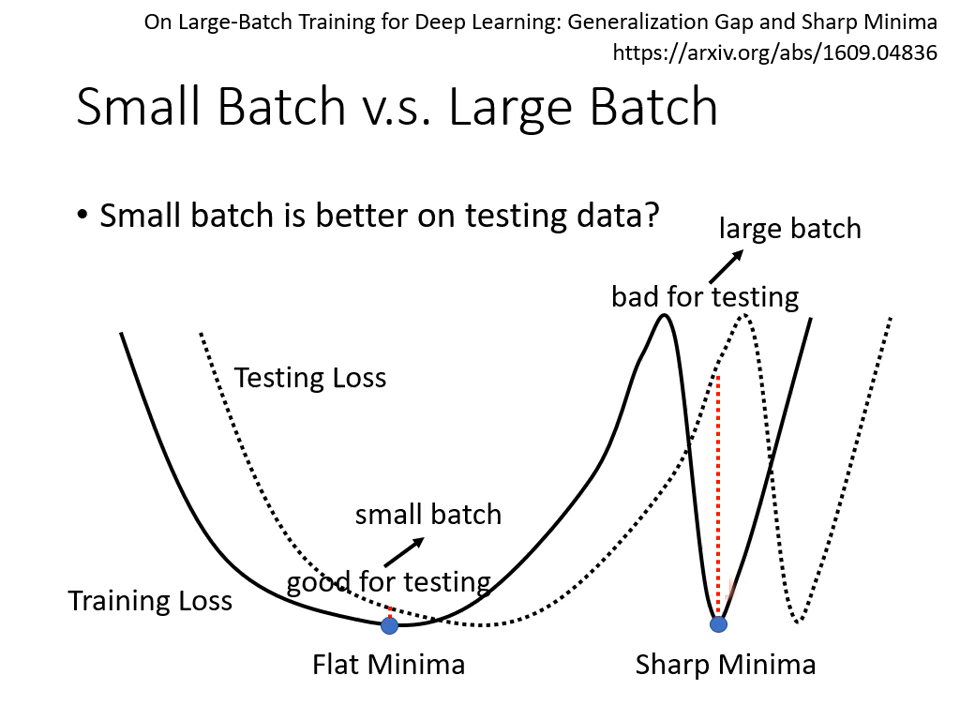
- 泛化 (Generalization) 面:
- 峽谷 (Sharp Minima): 大批次容易走到窄而深的峽谷,一旦訓練與測試資料有微小偏差,Loss 就會暴增。
- 盆地 (Flat Minima): 小批次因為更新方向隨機,容易跳出窄峽谷,最後停留在寬廣的盆地。即便測試資料有偏移,Loss 依然能維持在低檔。
動量 (Momentum)
動量是另一種對抗臨界點(Local Minima 或 Saddle Point)的技術,其核心概念源自物理界的慣性。
- 物理類比: 想像參數是一顆從斜坡滾下的球。一般的梯度下降在遇到地勢平坦(Saddle Point)或小坑洞(Local Minima)時就會停下;但若球帶有動量,它能憑藉之前的速度翻過小坡,繼續尋找更低的點。
- 運作原理:
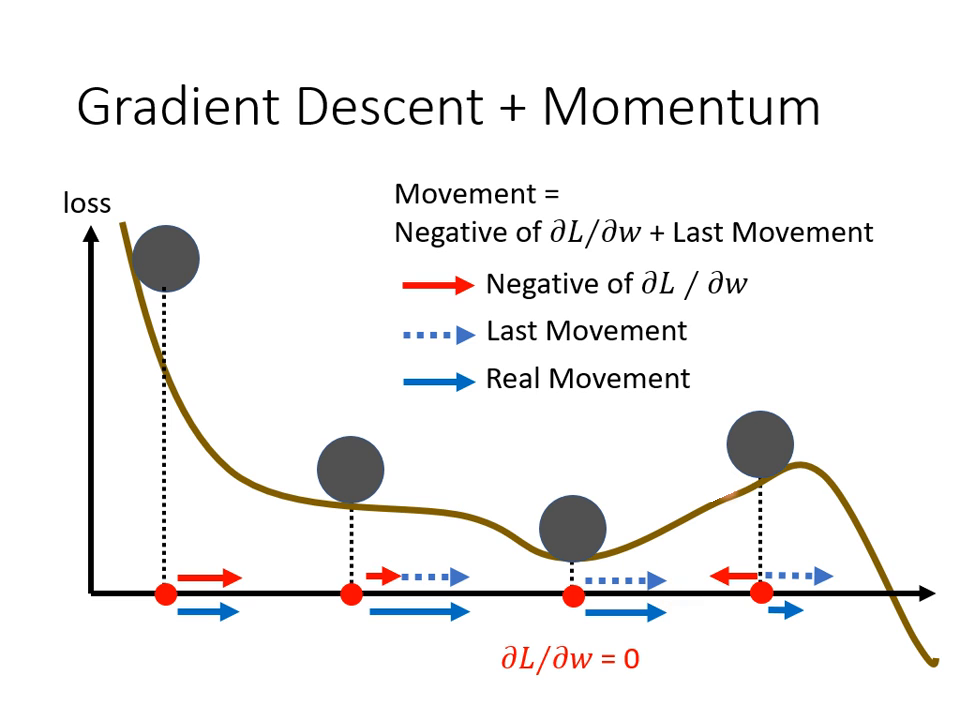
- 一般梯度下降: 只往梯度的反方向移動。
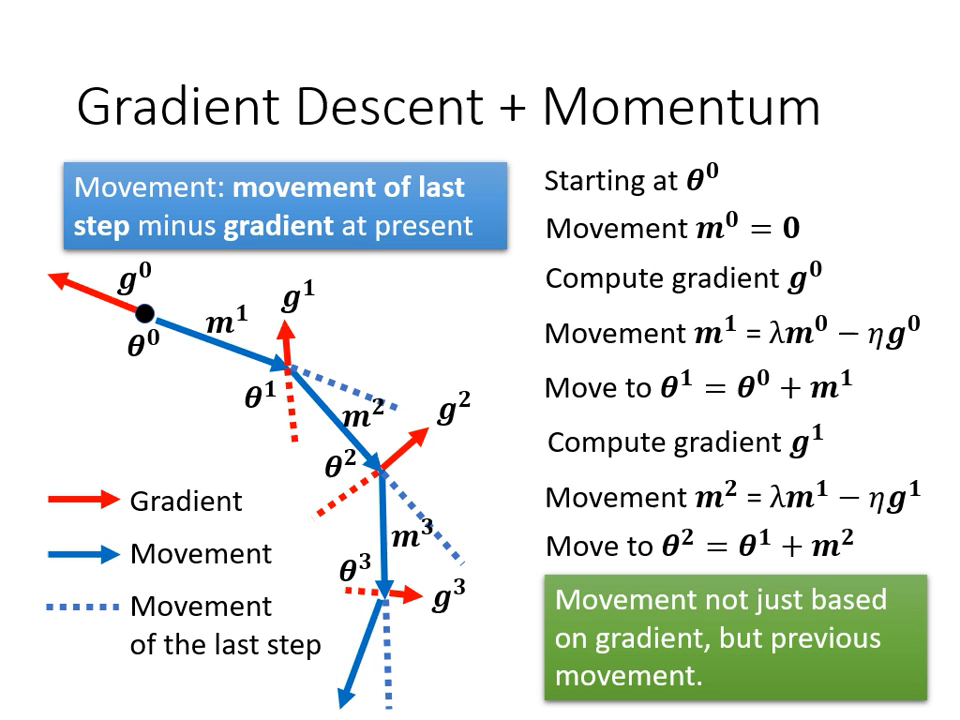
- 加入動量: 下一步移動的方向 = 「當前梯度的反方向」+「前一步移動的方向」。
- 數學解讀: 動量可以被看作是過去所有梯度之加權總和。這使得參數即使在梯度為零的地方,仍能靠著「之前的方向」繼續前進。
 |  |
|---|---|
| 參考物理現實 | 「當前梯度的反方向」+「前一步移動的方向」 |